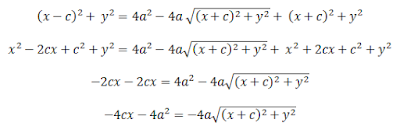BAB III. ELIPS, PARABOLA,DAN HIPERBOLA

hay sobat apa kabar?,,Alhamdulillah,pastinya baik dong....
Pada bab iv ini sobat kita akan membahas tentang elips,parabola dan hiperbola, sobat- sobat pasti pernah mendengar dan melihat bentuk-bentuk dalam kehidupan nyata dari yang sudah saya sebutkan tadi...?
nah untuk lebih paham lagi yukk!! baca langsung di blog kita ...⟱
bentuk elips dalam kehidupan nyata sobat pernah kan melihat gamba seperti ini,,

1. Elips

Elips adalah tempat kedudukan titik-titik yang jumlah jaraknya terhadap dua titik tertentu adalah tetap. Kedua titik tersebut adalah titik focus / titik api.

Persamaan Elips dengan Pusat O(0,0)
Perhatikan gambar di bawah ini !

Keterangan : 

• Pusat O(0,0) 

• Puncak A₁(a, 0) dan A₂(-a, 0) 

• Fokus F₁(c, 0) dan F₂(-c, 0) dengan a² = b² + c² 

• Sumbu simetri : sumbu X dan sumbu Y 

• Sumbu simetri yang melalui titik fokus F₁ dan F₂ disebut sumbu utama / sumbu transversal. 

• Sumbu simetri yang tegak lurus sumbu utama disebut sumbu sekawan. 

• Sumbu utama = 2a dan sumbu sekawan = 2b 

• Direktriks :  

• Eksentrisitas :

 

Titik F₁ dan F₂ disebut titik apu atau fokus.

AB disebut sumbu panjang : |AB| = 2a

CD disebut sumbu pendek

Titik-titik A, B, C dan D disebut puncak-puncak ellips.

|TF₁| + |TF₂| = PQ = 2a

Kedua ruas dikuadratkan :

Kedua ruas dikuadratkan lagi :

Karena a > 0 maka a² - c² > 0 maka a² - c² = b²

merupakan persamaan elips dengan pusat O(0,0) yang sumbu panjangnya 2b dan sejajar sumbu Y sedang sumbu pendeknya 2a dan sejajar sumbu X.

Persamaan Ellips diatas adalah

Dan 

Persamaan untuk Ellips diatas adalah

Persamaan Elips dengan Pusat ()

 
Contoh :
Tentukan : pusat, focus, sumbu simetri, sumbu panjang, sumbu pendek, direktriks, dan eksentrisitas dari persamaan elips berikut ini : x² + 4y² – 4x + 24y + 4 = 0
jawab :


2. Hiperbola

Hiperbola adalah tempat kedudukan titik-titik yang selisih jarak titik itu terhadap dua buah titik tertentu mempunyai nilai yang tetap. Kedua titik tertentu itu disebut fokus dari hiperbola. 

a. Persamaan Elips dengan Pusat O(0,0)
Perhatikan gambar berikut ini !

 

• Pusat O(0,0)

• Fokus F₁(c, 0) dan F₂(-c, 0) dengan c² = a² + b² 

• Titik puncak A₁(a, 0) dan A₂(-a, 0), selisih jarak = 2a dengan c > a

• Persamaan direktriks :  

• Persamaan asymtot ;

merupakan persamaan hiperbola dengan pusat O(0,0) yang sumbu utama pada sumbu Y

 b. Persamaan Hiperbola
 
 

 

 2.  Aplikasi Hiperbola

•   Hiperbola sering muncul sebagai grafik dari persamaan-persamaan kimia, fisika, biologi dan ekonomi (Hukum Boyle, Hukum Ohm, kurva permintaan dan penawaran)

•   Sebuah aplikasi khusus dari hiperbola yaitu sistem navigasi pada Perang Dunia I and II

 

Contoh:
Diketahui hiperbola dengan persamaan dalam bentuk umum sebagai berikut : 9x² – 16y² – 18x – 64y – 199 = 0.
Tentukan :
a) Koordinat titik pusat d) persamaan garis asymtot
b) Koordinat titik focus e) Sketsa grafiknya
c) Koordinat titik puncak

Jawab:
Bentuk persamaan diubah ke dalam bentuk umum :

9x² – 16y² – 18x – 64y – 199 = 0

9x² – 18x – 16y² – 64y = 199

9(x² – 2x) – 16(y² + 4y) = 199

9(x – 1)² – 9 – 16(y + 2)² + 64 = 199

9(x – 1)² – 16(y + 2)² = 199 + 9 – 64

9(x – 1)² – 16(y + 2)² = 144

 

 


3. Parabola 

Parabola adalah tempat kedudukan titik-titik yang jaraknya sama terhadap suatu titik tertentu dan garis tertentu. Titik tertentu itu disebut titik api ( fokus ) dan garis tertentu itu disebut direktriks.

• Titik itu disebut fokus/titik api (F)

• Garis tertentu itu disebut garis direktris/garis arah

• Garis yang melalui F dan tegak lurus dengan garis arah disebut sumbu simetri parabola

• Titik potong parabola dengan sumbu simetri disebut puncak parabola

• Tali busur terpendek yang melalui F disebut Latus Rectum → tegak lurus dengan sumbu simetri

Contoh gambar:

 

Contoh  :

Diketahui parabola y² – 6y – 8x + 1 = 0, tentukanlah puncak, sumbu simetri, dan fokusnya !

Jawab :

• Pertama, persamaan yang diketahui diubah ke bentuk baku yaitu : (y – b)² = 4p(x – a) dengan     cara melengkapkan kuadrat sempurna.

Langkah – langkahnya :

Kita tulis terlebih dahulu persamaan yang diketahui :

y² – 6y – 8x + 1 = 0

Suku yang mengandung y kita kumpulkan di ruas kiri :

y² – 6y = 8x – 1

• kedua ruas ditambah dengan 9 ( nahhh….ini yang bikin bingung kan. Mengapa ditambah 9?. Agar di ruas kiri berbentuk kuadrat sempurna. Ingat kembali materi tentang melengkapkan kuadrat sempurna). Sehingga :

y² – 6y + 9 = 8x – 1 + 9

suku yang di ruas kiri kita ubah ke dalam bentuk kuadrat sempurna.

(y – 3)² = 8x + 8

Selanjutnya kita ubah ke dalam bentuk baku persamaan parabola, sehingga :

(y – 3)² = 8(x – (-1))

Dari persamaan terakhir ini kita dapatkan bahwa puncaknya adalah

P (a, b) P (-1, 3)

Fokus F (p + a, b) F(2 – 1, 3) = F (1,3)

Sumbu Simetri y = b y = 3.



Semoga bermanfaat,masih banyak yang kurang masih jauh dari kata sempurna,terima kritik dan saranya teman-teman!!!!!