BAB I SISTEM KOORDINAT KARTESIEN TEGAK LURUS DAN PERSAMAAN GARIS LURUS

Geometri analitik merupakan kajian terhadap obyek-obyek geometri dengan menggunakan sistem koordinat yang diulas menggunakan konsep dan prinsip aljabar dan analisis.Perkembangan geometri analitik dimulai dengan kehadiran bentuk baru persamaan (equation) Bentuk baru persamaan tersebut memungkinkan untuk mengklasifikasikan kurva berdasarkan derajat (degree). Kurva berderajat satu adalah garis lurus (straight lines), kurva berderajat dua merupakan irisan kerucut (conic sections), dan kurva berderajat tiga dinamakan kurva kubik (cubic curves).

 

Sebelum kita membahas tentang titik dan kurva pada sistem koordinat kartesius. Nah sobat, pada belum tahukan?? Apa yang dimaksud dengan koordinat katesian itu? Koordinat kartesius petama kali ditemukan oleh Descartes (sekitar tahun 1637)  menggunakan bentuk baru persamaan tersebut untuk mengubah masalah-masalah geometri menjadi masalah aljabar menggunakan koordinat sehingga dapat diselesaikan dengan manipulasi aljabar dimana untuk menentukan letak atau posisi pada bidang datar diberikan suatu patokan yang terdiri dari dua garis yang saling tegak lurus,yaitu garis horizontal disebut sumbu x dan garis vertikal disebut sumbu y.      

    

Baikalah sobat, sudah pahamkan sistem koordinat kartesius itu apa, pasti sudah paham dong!!Selanjutnya nih sobat..!!  kita akan membahas tentang titik dan kedudukan titik – titik berdasarkan teorema dasar .

•         Titik adalah suatu objek yang tidak terdefinisi, tidak memiliki besaran ,tidak memiliki panjang, maupun ketinggian dan mempunyai kedudukan yang dilambangkan dengan tanda (noktah),serta mempunyai letak atau posisi. Dimana Posisi dijadikan acuan untuk menentukan suatu subjek.

•         Titik-titik pada sebuah bidang yang membentuk himpunan titik dan memenuhi suatu kriteria tertentu dinamakan kedudukan titik (locus of points)

 Oh iya sobat ada juga loh,Teorema-teorema dasar tentang kedudukan titik-titik (Fundamental Locus Theorems) yang biasa digunakan sebagai berikut.

1)   Teorema 1.1

Ada titik P yang dikelilingi oleh banyak titik lain yang berjarak sama yaitu d sehingga membentuk lingkaran yang berpusat dititik P.


2)   Teorema 1.2

Kedudukan titik-titik yang berjarak sama yaitu d dari sebuah garis l  adalah sepasang garis-garis sejajar yang masing-masing berjarak d dari garis l.

3)   Teorema 1.3

Kedudukan titik-titik yang berjarak sama (equidistant) dari dua buah titik P dan Q adalah sebuah ruas garis (disebut perpendicular bisector).yang tegak lurus  terhadap ruas garis  dan membagi  menjadi dua bagian sama besar


4)   Teorema 1.4

Kedudukan titik-titik yang berjarak sama dari dua garis yang sejajar yaitu l₁ dan l₂ merupakan sebuah garis diantara keduanya dan sejajar dengan kedua garis tersebut.


5)   Teorema 1.5

Kedudukan titik-titik yang berjarak sama terhadap dua garis yang berpotongan yaitu l₁ dan l₂, adalaha sepasang ruas garis (disebut bisectors) yang membagi dua sama besar sudut-sudut yang yang dibentuk garis l₁ dan l₂


6)   Teorema 1.6

Kedudukan titik-titik yang berjarak sama dari kedua sisi sebuah sudut adalah sebuah ruas garis yang membagi dua sudut tersebut (bisector of angle)


7)   Teorema 1.7

Kedudukan titik-titik yang berjarak sama dari dua buah lingkaran konsentris (concentric circles) adalah sebuah lingkaran yang konsentris terhadap kedua lingkaran tersebut dan berada tepat di tengah keduanya


8)   Teorema 1.8

Kedudukan titik-titik pada jarak tertentu dari sebuah lingkaran yang memiliki jari-jari lebih panjang dari jarak tersebut merupakan sebuah pasangan lingkaran konsentris, di mana masing-masing kedudukan titik tersebut berada di salah satu sisi lingkaran pada jarak tertentu tersebut.


9)    Teorema 1.9

Kedudukan titik-titik yang berjarak tertentu dari suatu lingkaran berjari-jari kurang dari jarak tersebut merupakan sebuah lingkaran yang berada di luar lingkaran pertama dan saling konsentris.

CONTOH  PEMBUKTIAN p : Kedudukan titik-titik pada suatu ruas garis berjarak sama dari P dan Q q : Ruas garis tegak lurus PQ dan membagi PQ menjadi 2 bagian sama panjang
Diketahui : -Titik P dan titik Q -Ruas garis AB tegak lurus PQ dan membagi ruas garis PQ Ditanya : Misalk sembarang titik di AB dalah C, C berjarak sama ke PQ yaitu ?
PENYELESAIAN :

 
nah sobat kita sudah tahukan teorema-teorema dasar kedudukan titik, maka dari teorema-teorema itu kita dapat menyelesaikan dan mengaitkan suatu masalah kedalam teorema tersebut seperti contoh dibawah ini :  

Pertanyaan 2 - 1 :     Jika titik-titik tersebut dihubungkan dengan ruas garis maka diperoleh sebuah segiempat CDAB, hitunglah luas dan keliling segiempat tersebut.

Penyelesaian :

Diketahui      :    Segiempat CDAB dengan koordinat A(1, 2), B(-3, 4), C(-3, -1), D(1, -1) 

Ditanyakan   :    Luas CDAB = …………satuan luas

 

Identifikasi masalah   :    Untuk memudahkan penyelesaian, perlu didentifikasi bentuk CDAB yaitu dengan cara menghubungkan semua titik sudut sehingga diperoleh bentuk di samping. Identifikasi bentuk menunjukkan bahwa CDAB merupakan sebuah trapesium siku-siku. Masalah luas dan keliling dapat diselesaikan apabila panjang sisi CDAB diketahui. Sisi CDAB yaitu ruas garis CD, DA, AB, dan BC. Panjang tiap ruas garis dapat ditentukan dengan menggunakan rumus jarak antara dua titik. Keliling CDAB adalah jumlah panjang semua sisi CDAB sehingga dirumuskan : . Luas ditentukan dengan menggunakan rumus luas trapesium yaitu setengah dari tinggi trapesium dikali jumlah panjang sisi-sisi sejajar sehingga dirumuskan :

Langkah Penyelesaian     :

Langkah 1) Menentukan panjang tiap sisi CDAB

Langkah 2) Menentukan keliling CDAB

satuan panjang

Langkah 3) Menentukan luas CDAB

 satuan luas

Jadi luas segiempat CDAB yaitu 16 satuan luas dan keliling CDAB sekitar 17,47 satuan panjang

Teorema 1.10 :

Koordinat titik tengah P(x, y) pada sebuah ruas garis yang titik-titik ujungnya adalah A(x₁, y₁) dan B(x₂, y₂) adalah x = ½ (x₁+ x₂) dan y = ½ (y₁ + y₂)

Pembuktian teorema terdapat pada buku Geometri Analitik Bidang dan Ruang PGMT3839/3SKS Modul1-9 (Sukirman, 1994 : 5)

Teorema 1.11 :

Apabila diketahui titik-titik P(x₁, y₁) dan Q(x₂, y₂) serta titik T(x, y) pada ruas garis  sedemikian sehingga  maka koordinat titik T ditentukan oleh :

    dan   

Pembuktian teorema terdapat pada buku Geometri Analitik Bidang dan Ruang PGMT3839/3SKS Modul1-9 (Sukirman, 1994 : 6 - 7)

 

Dalam diagram kartesius, dilibatkan dua garis yang tolok ukur dalam penentuan posisi atau letak suatu titik. Dua garis ini letaknya saling tegak lurus dengan titik pusat (0,0), yang selanjutnya disebut sumbu koordinat. Sumbu vertikal disebut dengan pasangan absis x dan sumbu horizonal disebut ordinat y.

Persamaan Garis Lurus digambarkan dalam bentuk :

Dalam Persamaan garis lurus sobat, dikenal dengan istilah Gradien. Gradien adalah Perbandingan antara komponen x (absis) dan komponen y (ordinat) antara dua titik pada garis itu. Gradien juga dikenal sebagai koefisien arah pada garis lurus yang dilambangkan dengan huruf m. Gradien terbagai menjadi beberapa nih sobat yakni :

• Gradien garis yang melalui Titik Pusat (0,0) dan Titik (x,y). Misalnya nih, diketahui sebuah titik (2,4).Nah Berapakah persamaan garis yang melalui titik pusat? Dari permasalahan ini, penyelesaian adalah Persamaan garis (0,0) dan (2,4) ialah y = 4/2x <=> y = 2x, sehingga gradiennya adalah 2.
• Gradien garis yang melalui Dua Buah Titik (x1,y1) dan (x2,y2). Dalam hal ini berlaku fungsi :

 

• Gradien Garis Yang Sejajar Sumbu-X dan Sumbu-Y.  Dalam kondisi ini, gradien garis  yang sejajar dengan sumbu-y tidak didefinisikan.
• Gradien Garis Yang Saling Sejajar
• Gradien Garis Yang Tegak Lurus  

B. Persamaan Garis Lurus  

1. Persamaan Garis Lurus bentuk umum ( y = mx ) persamaan yang melalui titik pusat ( 0 , 0 ) dan     bergradien m . Contoh :

          Tentukan persamaan garis lurus yang melalui titik pusat ( 0 , 0 ) dan bergradien 2 !

          Jawab : y = mx

           y = 2 x 

    2. Persamaan Garis Lurus bentuk y = mx + c , Persamaan garis yang / / dengan y dan bergradien m .        Persamaan garis yang melalui titik ( 0 , c ) dan bergradien m .  ( 0 , c ) adalah titik potong sumbu y.

    3. Persamaan Garis Lurus Yang Melalui titik ( x1 , y1 ) dan bergradien m . persamaannya yaitu :

y – y1 = m ( x – x1 ) 

    4. Persamaan Garis Lurus Yang Melaui Dua titik yaitu  ( x1 , y 1 ) dan ( x2 , y2 ) .

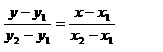contoh :

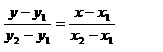
1. Persamaan garis lurus yang melalui titik ( 0 , -2 ) dan m = 3/4 adalah . . .

jawab:

Diketahui :

titik garis ( 0 , -2 )

m = 3 / 4

Ditanya :

Persamaan garis = . . .?

Jawab :

cara 1

y = mx + c

y = 3/4 x  + ( -2 )   x4

< => 4y = 3x – 8

< = > -3x + 4y + 8 = 0

cara 2

y – y1 = m ( x – x1 )

y – ( -2 ) = 3/4 ( x – 0 )

y + 2 = 3/4 x     x4

< = > 4y + 8 = 3x

< = > -3y + 4y + 8

Demikian penjelasan mengenai rumus persamaan garis lurus . Semoga dengan penjelasan di atas , sedikit membantu memecahkan permasalahan dalam mengerjakan soal yang berhubungan dengan persamaan garis lurus . Inti dari persamaan garis lurus adalah memahami apa itu gradien dan memahami antara titik yang dilalui baik titik pusat koordinat , titik koordinat y ataupun titik koordinat x .Atau jika dilambangkan yaitu titik pusat koordint ( 0 , 0 ) , titik koordinat ( x1 , y1 ) dan ( x2 , y 2 ) .

 

Semoga bermanfaat sobattt!!!! . . . .